Satellite Geodesy:Surveying the Earth from Orbit

Geodesy is the science that lets us where things are on Earth and where they are going.

Not where in the Universe.

Or where in the Multiverse.

Not where in the galaxy.

It's about where things are on Earth. It's very down to Earth in that sense 😀.

For example, where is the top of the world?
Image credit: AFP/Project Possible

Is it 8,848 m above sea level? Or 8,851 m? What even is sea level?
Image credit: AFP/Project Possible

Badwater Basin, Death Valley, USA: 85.5 m below sea level.

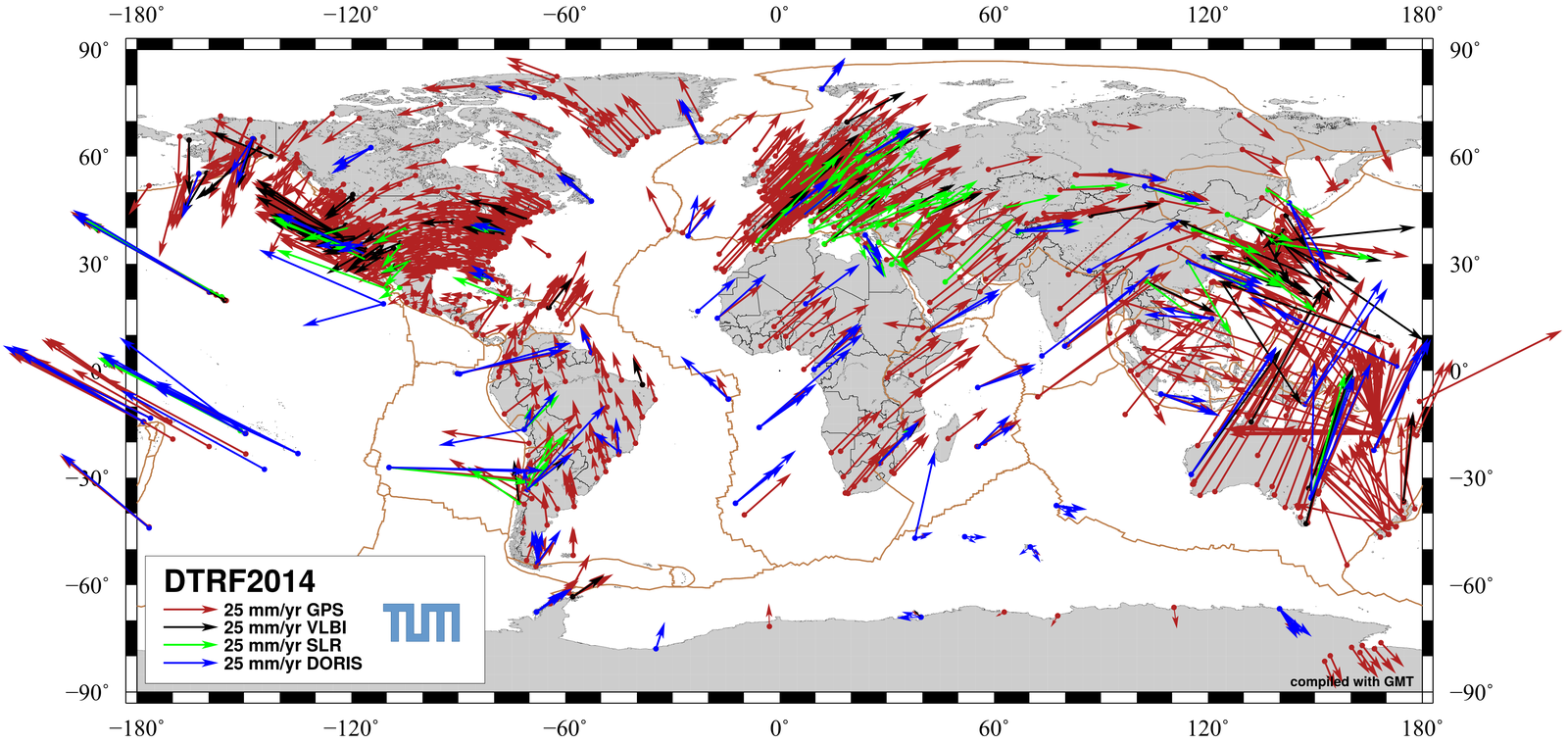
Earth Science: Monitoring Tectonic Plate Motion

Positioning & Navigation

Earth-centred Coordinate Systems

To label points on in 3D space we need a coordinate system

X, Y and Z axes with origin point at (x=0,y=0,z=0)

The origin should be at the Earth's centre of mass. But where is that?

Can we assume that the center of mass and the center of geometry are the same? What geometrical object best represents Earth's shape?

Mostly we are interested in where things are in relation to the Earth's surface.

Equation of a spherical surface: $$x^2+y^2+z^2=r^2$$

The Earth is not spherical. Geodesists model geometric shape of the Earth as oblate spheroid (or ellipsoid).

General equation for an ellipsoid: $$ \frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1 $$

Datums

Height Definition Method 1: Distance from the ellipsoid in the direction normal (or pependicular) to the reference ellipsoid (or datum).

Geodesists call this the ellipsoidal (or geodetic) height. But this is not the way the height above mean sea level is measured.

Method 2: Instead we use a gravitational equipotential surface. For example, suppose there is some surface where the acceleration due to gravity is \(9.8 m/s^2\).

The equipotential surface at mean sea level is known as the geoid (another datum). What the shape of this surface look like? Why do we care?

An added complication: The Earth is rotating in inertial space.

So we need two types of coordinate system: rotating (Earth-fixed) and non-rotating (Inertial).

Interesting fact: In the Earth-centered Inertial (ECI) system, we are flying through space at ~\( 300 \mathrm{ms^{-1}} \).

Measuring Earth's Gravity from Orbit

If the mass of the Earth is uniformly distributed: $$ \mathbf{a_{sc}} = -\frac{GM_E}{r_{sc}^2} \mathbf{\hat{r}_{sc}} $$

The orbital trajectory of low Earth orbiter (LEO) satellites (e.g. GOCE flying at ~300 km altitude, orbital speed ~7 km/s) are sensitive to deviations from a point mass model of Earth gravity.

Measuring Earth's Gravity from Orbit

Medium Earth Orbiter (MEO) satellites, such as the satellites of the Global Positioning System (GPS), fly at much higher altitudes of about 20,000 km.

Satellites like GOCE also carry GPS receivers onboard. So we can observe how their orbits deviate from the shape predicted simpler gravity models.

Gravity Field and Steady-State Ocean Circulation Explorer (GOCE)

The Geoid shape derived from GOCE observations

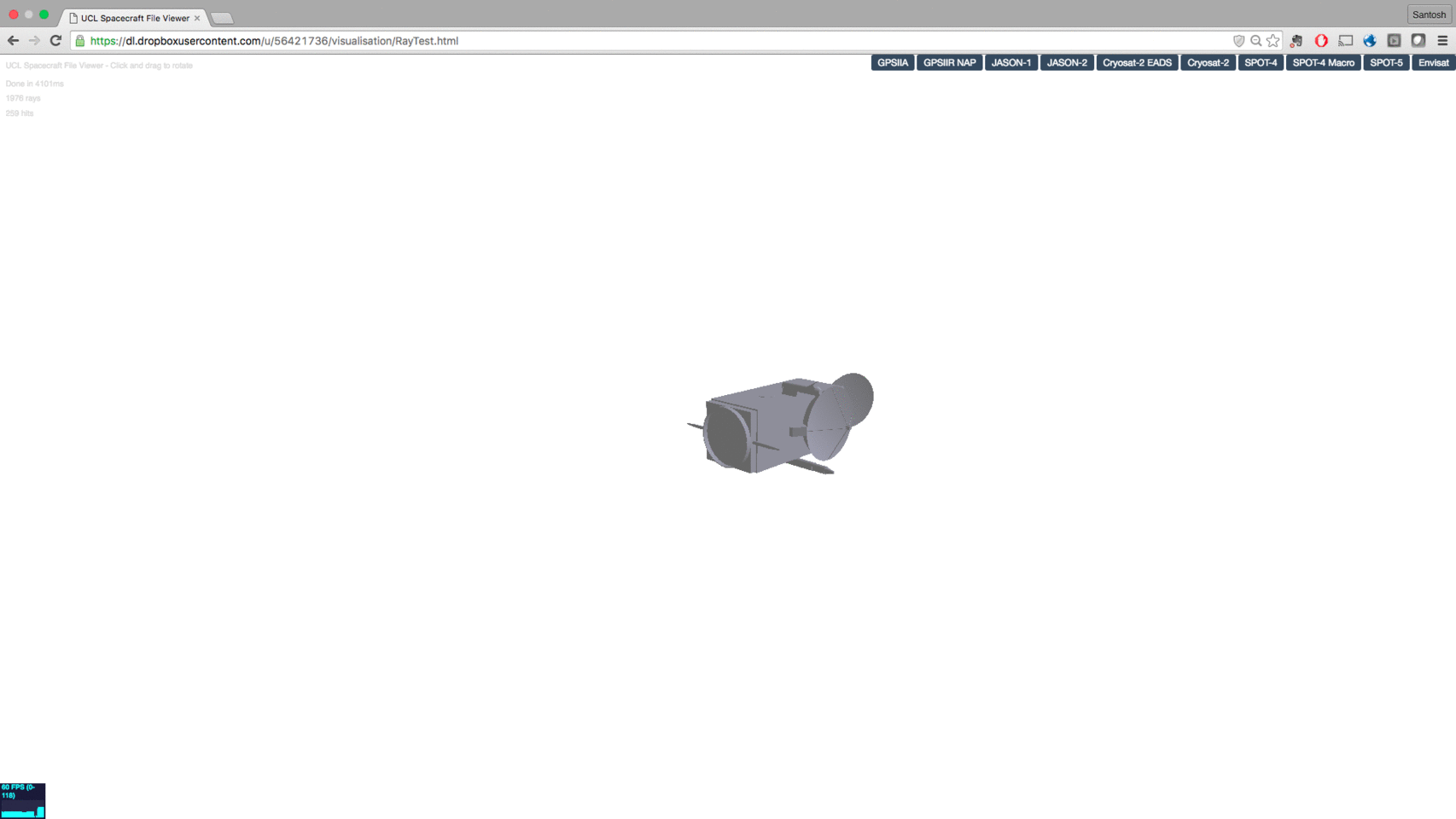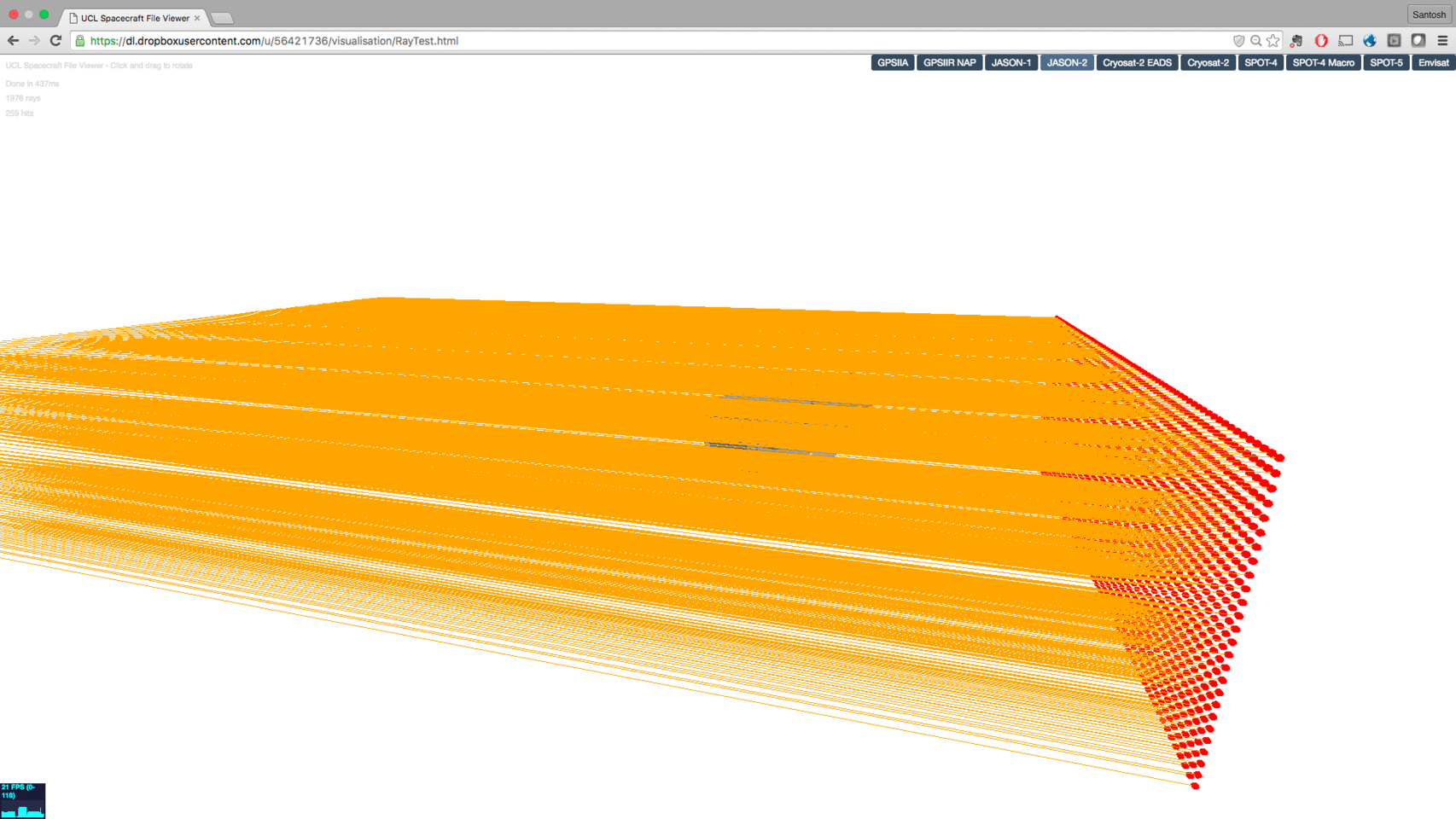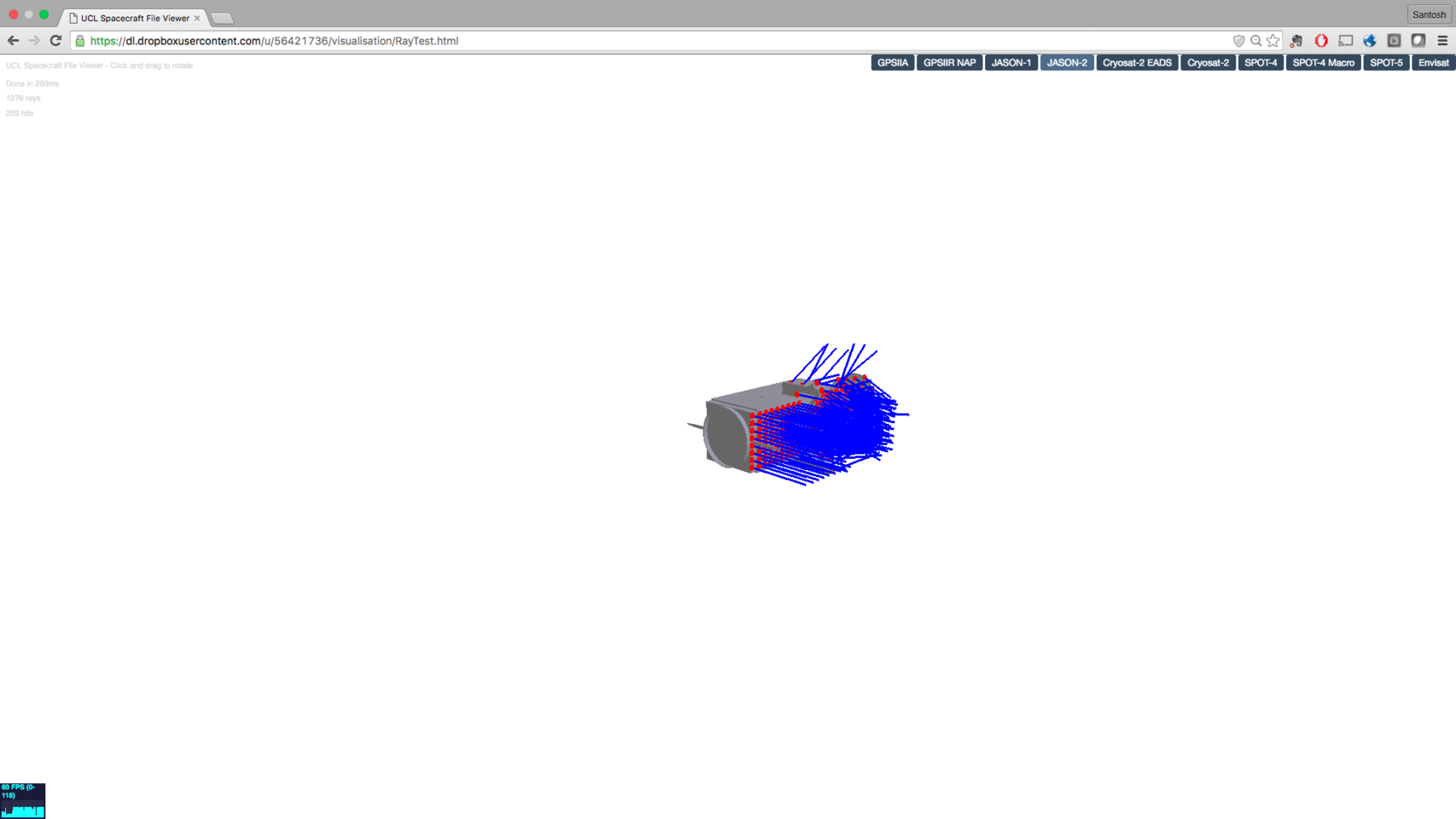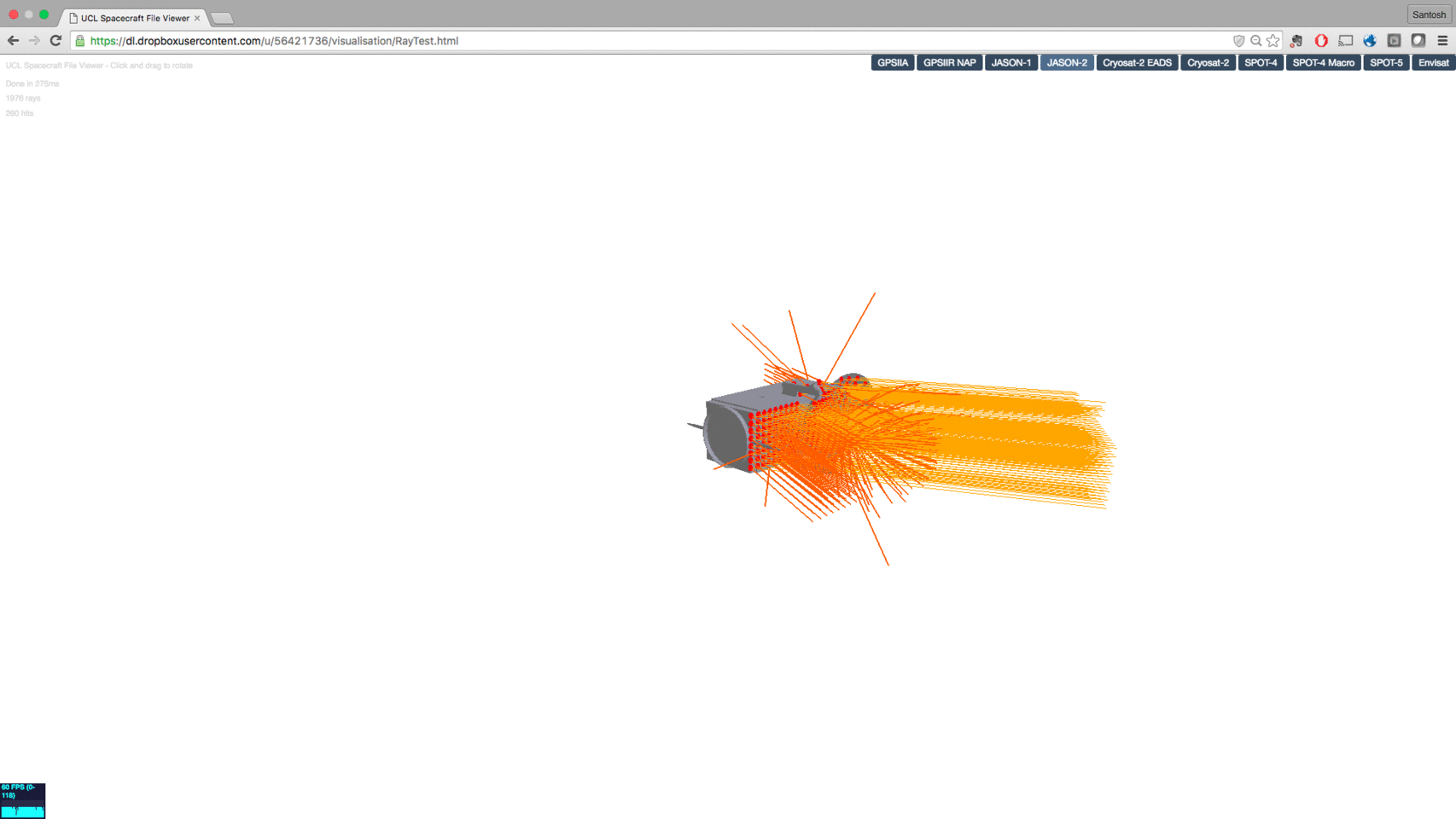
Our research at UCL: radiation force modelling for precise orbit determination of spcecraft

Thanks! s-bhattarai.github.io
toshie_B s-bhattarai

/

Go to slide: